Square root of prime number is an irrational number.

For any prime p ,    is an irrational number.

proof:-

     We will prove this by using contradiction. 

   Let us assume that  is a rational number. 

i.e. we can write    as    where a and b are integer and   .and a and b are coprime.(gcd (a,b)=1).

Now ,

           

 squaring on both sides,

               

                ------------------ (1)

    here we can say is multiple of p or  p divides i.e.     (as  ,p is prime )

    (we know that ,by Euclid's lemma, for any prime p if

              for any integer a,b)

    

   here  

         Since p is a prime number ,so if p divdes then p divides a.

  we can write a=np where n is any constant 

  i.e. a is multiple of p

  put this in equation (1) , 

    

   

           

     This implies p divides  , and as p is prime p also divides b (Euclid's lemma)

       We get prime p such that p divides a as well as b.  hence p is common factor of a and b 

Which contradicts that a and b are coprime. 

             This is due to our wrong assumption that  is rational number.

         This proves  is an irrational number.

But what if the number is composite. ???

Let us prove    is an irrational number.

proof :- 

          Contrary assume that   is rational number.

  Then we can write 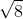 as         ---------- (1)   where a and b are integer with 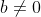 .and a and b are coprime.(gcd (a,b)=1).

          ( we will use Fundamental Theorem of Arithmetic, which states that Any positive integer >1 is itself a prime number or can be written as product of  prime numbers.)

 we write 

                         

                                                       (from (1))

                                       

                         
        Which is not possible As we prove above,   is a irrational number since 2 is prime number and As a and 2b are integer ( )      is a rational number.

             
  Hence our assumption is wrong .

             is an irrational number.

     Similarly we can prove the result for other composite irrational numbers.