Square root of prime number is an irrational number.

For any prime p ,    is an irrational number.

proof:-

     We will prove this by using contradiction. 

   Let us assume that  is a rational number. 

i.e. we can write    as    where a and b are integer and   .and a and b are coprime.(gcd (a,b)=1).

Now ,

           

 squaring on both sides,

               

                ------------------ (1)

    here we can say is multiple of p or  p divides i.e.     (as  ,p is prime )

    (we know that ,by Euclid's lemma, for any prime p if

              for any integer a,b)

    

   here  

         Since p is a prime number ,so if p divdes then p divides a.

  we can write a=np where n is any constant 

  i.e. a is multiple of p

  put this in equation (1) , 

    

   

           

     This implies p divides  , and as p is prime p also divides b (Euclid's lemma)

       We get prime p such that p divides a as well as b.  hence p is common factor of a and b 

Which contradicts that a and b are coprime. 

             This is due to our wrong assumption that  is rational number.

         This proves  is an irrational number.

But what if the number is composite. ???

Let us prove    is an irrational number.

proof :- 

          Contrary assume that   is rational number.

  Then we can write 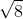 as         ---------- (1)   where a and b are integer with 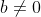 .and a and b are coprime.(gcd (a,b)=1).

          ( we will use Fundamental Theorem of Arithmetic, which states that Any positive integer >1 is itself a prime number or can be written as product of  prime numbers.)

 we write 

                         

                                                       (from (1))

                                       

                         
        Which is not possible As we prove above,   is a irrational number since 2 is prime number and As a and 2b are integer ( )      is a rational number.

             
  Hence our assumption is wrong .

             is an irrational number.

     Similarly we can prove the result for other composite irrational numbers.

Pythagoras formula

  In any Right angle  Triangle of side a,b,c        How????

                            Consider a square of side c and draw a four right angle triangle on each side in such a way that side of square is hypotenuse of a triangle as shown in fig,

                                             

                Now outer square is of length a+b so its area is . Here area of inner square of side c is and as we know area of trigle is 1/2*height*base. In this case the area of triangle becomes . so area of such four triangle is .

       Now area of outer square =  the sum of areas of inner sqaure and  four triangles. 

 It gives,

        

                                    Hence proved.

Square of the sum of two terms = square of 1st term + square of 2nd term + 2 × fist term × second term.

    But why??

solution :- Consider a arbitrary line and any arbitrary point on it such that point divides the line       segment  in two parts a & b. 

Then the length of this line is a+b . Now we want to find . so let's make a square of side a+b.

 

  Here, area of square of side a is  and area of square of side b is  . now remaining two rectangle of    side a & b and the Area of rectangle is a*b. therefore the area of two rectangle becomes  2ab. 

  So if we add area of all four parts of big square then we will get area of whole square. i.e

  area of square of side a+b is 

                              

        Hence proved. 

Similarly we can prove,  

                                       

 solution:-          Consider a arbitrary line of length a and take any arbitrary point on it at distance b then  the line divedes in two part as b and a-b .

Now make  square of length a. Then area of this square is sum of all area of all four parts. 

Here area of square of length a-b is and area of square of length b is. also the area of rectangle of side b and a-b is (a-b)*b . so area of such two rectangles becomes 2(a-b)*b.

 Therefore area of big square =
   

                                                 Hence proved.