solution :- Consider a arbitrary line and any arbitrary point on it such that point divides the line segment in two parts a & b.
Then the length of this line is a+b . Now we want to find ^{2}) . so let's make a square of side a+b.
. so let's make a square of side a+b.
Here, area of square of side a is 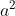 and area of square of side b is
and area of square of side b is 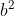 . now remaining two rectangle of side a & b and the Area of rectangle is a*b. therefore the area of two rectangle becomes 2ab.
. now remaining two rectangle of side a & b and the Area of rectangle is a*b. therefore the area of two rectangle becomes 2ab.
So if we add area of all four parts of big square then we will get area of whole square. i.e
area of square of side a+b is
Hence proved.
Similarly we can prove,
solution:- Consider a arbitrary line of length a and take any arbitrary point on it at distance b then the line divedes in two part as b and a-b .
Now make square of length a. Then area of this square is sum of all area of all four parts.
Here area of square of length a-b is ^{2}) and area of square of length b is
and area of square of length b is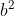 . also the area of rectangle of side b and a-b is (a-b)*b . so area of such two rectangles becomes 2(a-b)*b.
. also the area of rectangle of side b and a-b is (a-b)*b . so area of such two rectangles becomes 2(a-b)*b.
Therefore area of big square =
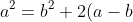b+(a-b)^{2}\\a^{2}=b^{2}+2ab-2b^{2}+(a-b)^{2}\\(a-b)^{2}=a^{2}-b^{2}-2ab+2b^{2}\\(a-b)^{2}=a^{2}-2ab+b^{2})
Hence proved.




Very nice and Interesting.
ReplyDelete